James Clerk Maxwell, autorul legilor de baza ale electrotehnicii

Se cauta 20 de ingineri si tehnicieni la o companie de echipamente electrice din Cluj
Compania Energom infiintata in urma cu zece ani, cu capital francez la Cluj, intentioneaza sa angajeze 20 de ingineri si tehnicieni, anul acesta. Astfel, compania va ajunge sa aibe 100 de salariati.
- Program Examen Autorizare ANRE - Primavara 2013
- Electricienii au cea mai mare stabilitate la serviciu
- Locuri de munca pentru inginerii romani, in strainatate
- Program Examen Autorizare ANRE -Toamna 2012
- Regulamentul Concursului National ''Electricianul Anului 2012 - SONEL''
- Profitul General Electric a scazut in primul trimestru
- ANRE organizeaza sesiunea de Primavara 2011 a examenului de autorizare a electricienilor
James Clerk Maxwell, autorul legilor de baza ale electrotehnicii
Astazi, 13 iunie 2012, se implinesc 181 de ani de la nasterea lui fizicianului James Clerk Maxwell, autorul unui set de ecuatii care descriu legile de baza ale electrotehnicii.

La 13 noiembrie 1831, la Edinburgh, in familia unui scotian înstarit, s-a nascut James Clerk Maxwell. Jocul întâmplarii a facut ca James sa se nasca în anul în care Faraday a descoperit fenomenul si legile inductiei, iar la maturitate sa se acopere de glorie cu lucrari teoretice strâns legate de studiul matematic al acestui fenomen. Activitatea lui s-a desfasurat într-un ritm sustinut, în domenii variate ale fizicii, si l-a condus la realizari de mare valoare.
J.C Maxwell dupa ce a studiat cercetariile in electricitate ale lui Faraday a pornit sa formuleze matematic o noua teorie a electricitatii si a magnetismului. El nu s-a putut folosi in demonstratiile sale de relativitate deoarece aceasta nu fusese inca descoperita, structura materiei era un mister iar relatia dintre lumina si electromagnetism nu era inca cunoscuta. In timp ce teoria lui Maxwell s-a dezvoltat termenul ∂E/∂t apare cu totul natural in formularea sa. El a denumit pe acesta “curent de deplasare”. Maxwell era interesat de campul magnetic in substanta solida ca si in vid si cand vorbeste despre un current de deplasare el include adesea o oarecare sarcina in miscare. Maxwell a gandit spatiul insusi ca un mediu,”eterul” in cat chiar si in absenta materiei solide curentul de deplasare aparea in ceva. Ecuatiile matematice ale lui Maxwell au fost perfect clare si neabigue si introducerea curentului de deplasare a fost o descoperire teoretica importanta. Descrierea campului electromagnetic realizat de Maxwell a fost in mod esential complet.
Traditionalele ecuatii ale lui Maxwell sunt :
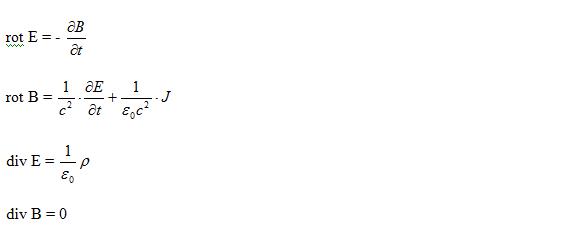
Aceste legi sunt scrise pentru campuri in vid in prezenta de sarcina electrica ρ si a curentului electric adica a sarcinii in miscare de densitate J.
Prima ecuatie este legea lui Faraday a inductiei . A doua exprima dependenta campului magnetic de densitatea curentului de deplasare sau rata de variatie a campului electric, si de densitatea curentului de conductie , sau viteza de miscare a sarcinii electrice. A treia este echivalenta cu legea lui Coulomb. A patra exprima ca nu exista surse de camp magnetic cu exceptia curentiilor.
Lipsa de simetrie in aceste ecuatii fata de B si E este in intregime datorita prezentei sarcinii electrice si a curentului electric de conductie. In vid termenii cu ρ si J sunt zero si ecuatiile lui Maxwell primesc urmatoarea forma:
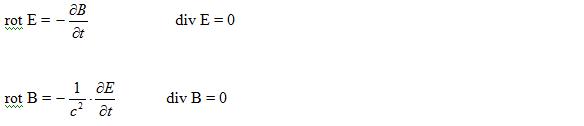
Aici termenul de current de depalasare este foarte important. Prezenta sa alaturi de analogul sau din prima ecuatie implica posibilitatea undelor electromagnetice. Recunoscand aceasta Maxwell a continuat sa dezvolte cu succes o teorie electromagnetica a luminii.
Putem arata acum ca o perturbatie electromagnetica in deplasare cu viteza c este compatibila cu ecuatiile lui Maxwell. Pentru a face aceasta vom descrie un aranjament simplu de campuri electrice si magnetice care reprezinta o perturbatie in deplasare si vom arata ca acestea satisfac ecuatiile lui Maxwell.
La momentul t=0 exista un camp electric in regiune dintre planele y=0 si y=2a. Aceasta intensitate a campului E are numai o componenta z si componenta sa z depinde numai de y, in urmatorul fel :

Dupa cum se indica in figura de mai jos aceasta descrie o distributie in forma de fronton a intensitatii campului maxima in centru in y = a si descrescand liniar pana la 0 in y = 0 si y = 2a. Pentru y dat campul este acelasi pentru toti x si y. Avem deci camp electric in toata regiunea dintre doua plane paralele . Portiunile umbrite insemnate 1 si 2 se afla in interiorul acestor plane. Oriunde in afara adica pentru y=0 si z=2a campul electric este 0 in acest moment de timp. In acelasi timp in aceasta regiune din spatiu exista si un camp magnetic care are doar o componenta x data de relatiile :
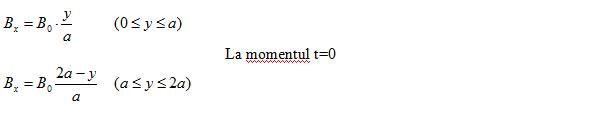
Sa facem acum configuratia de camp sa se deplaseze in directia y cu viteza c pastrandu-si forma aceasta o putem face scriind urmatoarele ecuatii: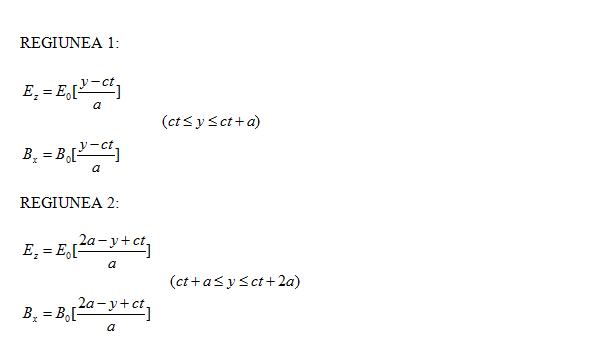
Aceasta descrie situatia asa cum o vedem in figura. Regiunea care contine campul este simplu deplasata spre dreapta prin distanta ct. In interiorul regiunilor 1 si 2 atat E cat si B au aceiasi forma ca inainte. Ecuatiile noastre descriu o configuratie in propagare de campuri electrice si magnetice dar noi trebuie sa vedem daca pot exista astfel de campuri. Pentru a raspunde la aceasta trebuie sa vedem daca E si B asa cum sunt date in ecuatiile de mai sus (din cele doua regiuni) satisfac ecuatiile lui Maxwell. Incepand cu ecuatiile de divergenta este usor de vazut ca div E =0 si div B=0. Dar rot E 0.
Ecuatiile conduc la exact aceiasi conditie pentru campurile in regiunea 1. Exact in varful frontonului si la fiecare capat exista singularitati matematice in campuri alese. Pentru a fi sigur ca ecuatiile de camp sunt satisfacute peste tot vedem ca nu exista nici o problema in aceste puncte, pentru ca E si B sunt continue acolo. Astfel campul electromagnetic particular pe care l-am descris care reprezinta o unda calatoare satisface toate ecuatiile de camp daca campul electromagnetic masurat in V/m este egal cu c ori intensitatea campului electromagnetic in Tesla in acelasi moment si in acelasi loc. Este esential ca E si B sa fie perpendiculare unul pe altul si pe directia de deplasare altfel aceste ecuatii de camp nu pot fi indeplinite.
Frontonul miscator ne poate surprinde ca un exemplu destul de speciat de unda. Aceste exemplu simplu ne arata tot ce este esential pentru orice unda electromagnetica. Dupa cum am mai aratat ecuatiile campului electromagnetic sunt liniare. Daca doua seturi de campuri satisfac ecuatiile lui Maxwell tot asa se intampla si cu suma lor.
Din ceea ce stim despre unda fronton trebuie sa se aplice la orice unda in care E si B sunt functii doar de coordonare de-a lungul directiei de miscare. Aceste date generale sunt:
a) distributia se deplaseaza cu viteza c cu forma neschimbatoare.
b) E si B sunt perpendiculare fiecare pe celalalt si pe directia de deplasare cu vectorul E*B totdeauna orientat in directia de deplasare asa cu mse intampal in exemplul nostrum
c) Intr-un punct dat si al un moment dat E=cB.
Un camp electromagnetic cu aceste proprietati se transforma in mod simplu si rezonabil cand schimbam sistemele de coordonate.
| 13/06/2012 - Acest articol a fost citit de 5699 ori | Tweet Recomanda |
|
Nota acordata: 3 (data de 251 vizitatori)
|
| Produse si servicii ale companiilor | Companiile active sunt aici |
| Alte stiri din categoria "Oameni de stiinta" |

|
|
||||||||||
 |
| TOP STORY |
Noua BSP41 pentru identificarea simplă a tablourilor electrice

Tablourile electrice pot fi identificate acum mai eficient cu noua imprimantă de identificare a firelor și tablourilor BSP41.
Identificați toate blocurile terminale
Noua imprimantă de identificare a firelor și tablourilor BSP41 poate imprima pe etichete de identificare rigide pentru toate mărcile majore de blocuri terminale și componente pentru tablouri electrice. Cu BSP41, constructorii de tablouri nu mai au nevoie de câte o imprimantă de etichete rigide pentru fiecare marcă utilizată. Brady Corporation oferă o listă de mărci de blocuri terminale care au fost testate în privința compatibilității cu noua BSP41.